Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
В
теме «Определенный интеграл» было
рассмотрено понятие определенного
интеграла
для случая конечного промежутка
и ограниченной функции
(см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
1.
Если, используя формулу для длины дуги,
попытаться вычислить длину четверти
окружности
,
,
то придем к интегралу от неограниченной
функции:
,
где
.
2.
Пусть тело массой
движется
по инерции в среде с силой сопротивления
,
где
- скорость тела. Используя второй закон
Ньютона (
,
где
ускорение),
получим уравнение:
,
где
.
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функция
Если
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда
,
то придем к интегралу по бесконечному
промежутку:
§1. Несобственные интегралы 1-го рода
I Определение
Пусть
функция
определена и непрерывна на промежутке
.
Тогда для любого
она интегрируема на промежутке
,
то есть существует интеграл
.
Определение
1
.
Конечный или бесконечный предел этого
интеграла при
называют несобственным интегралом 1-го
рода от функции
по промежутку
и обозначают символом
.
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (
или не существует) – расходящимся.
Итак, по определению
|
|
Примеры
2.
.
3.
– не существует.
Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.
II Формула Ньютона – Лейбница для несобственного интеграла первого рода
Пусть
- некоторая первообразная для функции
(сущест-вует на
,
т.к.
- непрерывна). Тогда
Отсюда
ясно, что сходимость несобственного
интеграла (1) равносильна существованию
конечного предела
.
Если этот предел обозначить
,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
,
где
.
Примеры .
5.
.
6.
Более сложный пример:
.
Сначала найдем первообразную:
Теперь
можем найти интеграл
,
учитывая,
что
:
III Свойства
Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:
IV Другие определения
Определение
2
.
Если
непрерывна
на
,
то
.
Определение
3
.
Если
непрерывна
на
,
то принимают по определению
(
–
произвольное),
причем несобственный интеграл в левой части сходится, если только оба ин-теграла в правой части сходятся.
Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.
Пример 7 .
§2. Признаки сходимости несобственного интеграла 1-го рода
Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство
(для
больших
).
Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.
I Интегралы от положительных функций
Пусть
на
.
Тогда определенный интеграл
как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
Теорема
1
.
Несобственный интеграл 1 го
рода от неотрицательной функ-ции сходится
тогда и только тогда, когда функция
остается
ограниченной при увеличении
.
Эта теорема – следствие общих свойств монотонных функций. Практического смысла теорема почти не имеет, но позволяет получить т.н. признаки сходимости.
Теорема
2
(1-й признак сравнения). Пусть функции
и
непре-рывны на
и удовлетворяют неравенству
.
Тогда:
1)
если интеграл
сходится, то и
сходится;
2)
если интеграл
расходится, то и
расходится.
Доказательство
.
Обозначим:
и
.
Так как
,
то
.
Пусть интеграл
сходится, тогда (в силу теоремы 1) функция
‒ ограничена. Но тогда и
ограничена,
а значит, интеграл
тоже сходится. Аналогично доказывается
и вторая часть теоремы.
Этот
признак не применим в случае расходимости
интеграла от
или сходимости интеграла от
.
Этот недостаток отсутствует у 2-го
признака сравнения.
Теорема
3
(2-й признак сравнения). Пусть функции
и
непрерывны и неотрицательны на
.
Тогда, если
при
,
то несобственные интегралы
и
сходятся или расходятся одновременно.
Доказательство . Из условия теоремы получим такую цепочку равно-сильных утверждений:
,
,
.
Пусть,
например,
.
Тогда:
Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.
В
качестве эталонной функции, с которой
сравнивают данную, высту-пает степенная
функция
,
.
Предлагаем студентам самим доказать,
что интеграл
сходится
при
и расходится при
.
Примеры
.
1.
.
Рассмотрим
подынтегральную функцию на промежутке
:
,
.
Интеграл
сходится, ибо
.
По 2-му признаку сравнения сходится и
интеграл
,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
2.
.
Так
как
,
тоcуществует
такое, что при
.
Для таких значений переменной:
Известно, что логарифмическая функция растет медленнее степенной, т.е.
,
а значит, начиная с некоторого значения переменной, эта дробь меньше 1. Поэтому
.
Интеграл
сходится как эталонный. В силу 1-го
признака сравнения сходится и
.
Применяя 2-й признак, получим, что и
интеграл
сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
Несобственные интегралы
Лк5,6(4ч)
Понятие было введено в предположении, что:
1) промежуток интегрирования конечен (отрезок [a ;b ]),
2) функция f (x ) ограничена на [a ;b ].
Такой определенный интеграл называется собственным (слово ²собственный² опускают). Если какое-либо из этих условий не выполняется, то определенный интеграл называется несобственным . Различают несобственные интегралы I и II рода.
1.Определение несобственного интеграла первого рода
Обобщим понятие определённого интеграла на бесконечный промежуток. Пусть f (x ) определена на промежутке [a ;+¥) и интегрируема в каждой конечной его части, т. е. . В этом случае существует интеграл . Ясно, что есть функция, определённая на [a ;+¥). Рассмотрим . Этот предел может существовать и не существовать, но независимо от этого он называетянесобственным интегралом первого рода и обозначается .
Определение. Если существует и конечен, то несобственный интеграл называется сходящимся , а значение этого предела есть значение несобственного интеграла. . Если не существует или равен ¥, то несобственный интеграл называется расходящимся .
Аналогично определяются ,
Пример 1. Исследовать на сходимость интеграл , .
D непрерывна на [a ;+¥) .
Если , то , а Þ интеграл сходится.
Если , то интеграл расходится.
Итак , сходится при и ;
расходится при .D
2. Свойства несобственного интеграла первого рода
Так как несобственный интеграл определяется как предел интеграла Римана, то на несобственный интеграл переносятся все свойства, которые сохраняются при предельном переходе, то есть выполняются свойства 1-8. Теорема о среднем значении не имеет смысла.
3. Формула Ньютона – Лейбница
Пусть функция f непрерывна на [a ;+¥), F - первообразная и существует . Тогда справедлива формула Ньютона – Лейбница:
В самом деле,
Пример 2. D . D
Геометрический смысл несобственного интеграла I рода
Пусть функция f неотрицательна и непрерывна на [a ;+¥) и несобственный интеграл сходится. равен площади криволинейной трапеции с основанием [a ;b ], а равен площади с основанием [a ;+¥).
4. Несобственные интегралы от неотрицательных функций
Теорема 1. Пусть f (x )³0 на [a ;+¥) и интегрируема на [a ;b ] "b >a . Для сходимости несобственного интеграла необходимо и достаточно, чтобы множество интегралов было ограничено сверху, причём .
Доказательство.
Рассмотрим функцию , a £b . Так как f (x )³0, то F не убывает Действительно, "b 1 , b 2: a £b 1 <b 2 в силу того, что , выполнено
По определению несобственный интеграл сходится тогда и только тогда, когда существует конечный . Т.к. F (b ) не убывает, то этот предел существует тогда и только тогда, когда функция F (b ) ограничена сверху, то есть $М >0: "b >a . При этом
Расходимость несобственного интеграла означает, что , то есть .
Теорема 2. Пусть функции f и g неотрицательны на [a ;+¥) и интегрируемы на [a ;b ] "b >a . Пусть на [a ;+¥) выполнено
1) из сходимости интеграла (2) следует сходимость интеграла (3);
2) из расходимости интеграла (3) следует расходимость интеграла (2).
Доказательство.
Из (1) "b >a .
1) Пусть интеграл (2) сходится. По теореме 1 множество ограничено ограничено ограничено. По теореме1 сходится.
2) Пусть расходится. Докажем, что расходится интеграл (2). От противного. Предположим, что интеграл (2) сходится, но тогда по первой части теоремы сходится интеграл (3) – противоречие с условием.
Теорема 3. Пусть функции f и g неотрицательны на [a ;+¥) и интегрируемы на [a ;b ] "b >a . Если существует (0£k £¥), то
1) из сходимости интеграла при k <¥ следует сходимость интеграла ,
2) из расходимости интеграла при k >0 следует расходимость интеграла .
Доказательство.
1) Пусть k <¥ и сходится.
Т. к. сходится, то сходится, значит, сходится . Тогда в силу (4) сходится . Отсюда сходится.
2) Пусть k >0 и расходится. В этом случае - конечное число. Если допустим противное – что интеграл сходится, то по доказанному в п. 1) получим, что тоже сходится, а это противоречит условию. Следовательно, сделанное предположение неверно, и расходится. сходится абсолютно, то по определению сходится . Значит, сходится. Но сходится.
Определенный интеграл
\[ I=\int_a^bf(x)dx \]
был построен в предположении, что числа $a,\,b$ конечны и $f(x)$ - непрерывная функция. Если одно из этих предположений нарушается, говорят о несобственных интегралах.
10.1 Несобственные интегралы 1 рода
Несобственный интеграл 1 рода возникает, когда по крайней мере одно из чисел $a,\,b$ бесконечно.
10.1.1 Определение и основные свойства
Рассмотрим сначала ситуацию, когда нижний предел интегрирования конечен, а верхний равен $+\infty$, другие варианты обсудим несколько позднее. Для $f(x)$, непрерывной при всех интересующих нас $x$, рассмотрим интеграл
\begin{equation} I=\int _a^{+\infty}f(x)dx. \quad(19) \label{inf1} \end{equation}
Прежде всего надо установить смысл этого выражения. Для этого введем функцию
\[ I(N)=\int _a^{N}f(x)dx \]
и рассмотрим ее поведение при $N\rightarrow +\infty$.
Определение. Пусть существует конечный предел
\[ A=\lim_{N \rightarrow +\infty}I(N)=\lim_{N \rightarrow +\infty}\int _a^{N}f(x)dx. \]
Тогда говорят, что несобственный интеграл 1 рода (19) является сходящимся и ему приписывают значение $A$, саму функцию называют интегрируемой на интервале $\left[ a, \, +\infty \right)$. Если же указанного предела не существует или он равен $\pm \infty$, то говорят, что интеграл (19) расходится.
Рассмотрим интеграл
\[ I=\int _0^{+\infty} \frac{dx}{1+x^2}. \]
\[ I(N)=\int _0^{N} \frac{dx}{1+x^2}. \]
В данном случае известна первообразная подинтегральной функции, так что
\[ I(N)=\int _0^{N} \frac{dx}{1+x^2}=arctgx|_0^{N}=arctgN. \]
Известно, что $arctg N \rightarrow \pi /2 $ при $N \rightarrow +\infty$. Таким образом, $I(N)$ имеет конечный предел, наш несобственный интеграл сходится и равен $\pi /2$.
Сходящиеся несобственные интегралы 1 рода обладают всеми стандартными свойствами обычных определенных интегралов.
1. Если $f(x)$, $g(x)$ интегрируемы на интервале $\left[ a, \, +\infty \right)$, то их сумма $f(x)+g(x)$ также интегрируема на этом интервале, причем \[ \int _a^{+\infty}\left(f(x)+g(x)\right)dx=\int _a^{+\infty}f(x)dx+\int _a^{+\infty}g(x)dx. \] 2. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right)$, то для любой константы $C$ функция $C\cdot f(x)$ также интегрируема на этом интервале, причем \[ \int _a^{+\infty}C\cdot f(x)dx=C \cdot \int _a^{+\infty}f(x)dx. \] 3. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right)$, причем на этом интервале $f(x)>0$, то \[ \int _a^{+\infty} f(x)dx\,>\,0. \] 4. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right)$, то для любого $b>a$ интеграл \[ \int _b^{+\infty} f(x)dx \] сходится, причем \[ \int _a^{+\infty}f(x)dx=\int _a^{b} f(x)dx+\int _b^{+\infty} f(x)dx \] (аддитивность интеграла по интервалу).
Справедливы также формулы замены переменной, интегрирования по частям и т.д. (с естественными оговорками).
Рассмотрим интеграл
\begin{equation} I=\int _1^{+\infty}\frac{1}{x^k}\,dx. \quad (20) \label{mod} \end{equation}
Введем функцию
\[ I(N)=\int _1^{N}\frac{1}{x^k}\,dx. \]
В данном случае первообразная известна, так что
\[ I(N)=\int _1^{N}\frac{1}{x^k}\,dx\,=\frac{x^{1-k}}{1-k}|_1^N= \frac{N^{1-k}}{1-k}-\frac{1}{1-k} \]
при $k \neq 1$,
\[ I(N)=\int _1^{N}\frac{1}{x}\,dx\,=lnx|_1^N= lnN \]
при $k = 1$. Рассматривая поведение при $N \rightarrow +\infty$, приходим к выводу, что интеграл (20) сходится при $k>1$, а при $k \leq 1$ - расходится.
Рассмотрим теперь вариант, когда нижний предел интегрирования равен $-\infty$, а верхний конечен, т.е. рассмотрим интегралы
\[ I=\int _{-\infty}^af(x)dx. \]
Однако этот вариант можно свести к предыдущему, если сделать замену переменных $x=-s$ и поменять затем пределы интегрирования местами, так что
\[ I=\int _{-a}^{+\infty}g(s)ds, \]
$g(s)=f(-s)$. Рассмотрим теперь случай, когда имеется два бесконечных предела, т.е. интеграл
\begin{equation} I=\int _{-\infty}^{+\infty}f(x)dx, \quad (21) \label{intr} \end{equation}
причем $f(x)$ непрерывна при всех $x \in \mathbb{R}$. Разобъем интервал на две части: возьмем $c \in \mathbb{R}$, и рассмотрим два интеграла,
\[ I_1=\int _{-\infty}^{c}f(x)dx, \quad I_2=\int _{c}^{+\infty}f(x)dx. \]
Определение. Если оба интеграла $I_1$, $I_2$ сходятся, то интеграл (21) называется сходящимся, ему приписывают значение $I=I_1+I_2$ (в соответствии с аддитивностью по интервалу). Если хотя бы один из интегралов $I_1$, $I_2$ расходится, интеграл (21) называется расходящимся.
Можно доказать, что сходимость интеграла (21) не зависит от выбора точки $c$.
Несобственные интегралы 1 рода с интервалами интегирования $\left(-\infty, \, c \right]$ или $(-\infty, \, +\infty)$ также обладают всеми стандартными свойствами определенных интегралов (с соответствующей переформулировкой, учитывающей выбор интервал интегрирования).
10.1.2 Признаки сходимости несобственных интегралов 1 рода
Теорема (первый признак сравнения). Пусть $f(x)$, $g(x)$ - непрерывны при $x>a$, причем $0 a$. Тогда
1. Если интеграл \[ \int _a^{+\infty}g(x)dx \] сходится, то сходится и интеграл \[ \int _a^{+\infty}f(x)dx. \] 2. Если интеграл \[ \int _a^{+\infty}f(x)dx \] расходится, то расходится и интеграл \[ \int _a^{+\infty}g(x)dx. \]
Теорема (второй признак сравнения). Пусть $f(x)$, $g(x)$ - непрерывны и положительны при $x>a$, причем существует конечный предел
\[ \theta = \lim_{x \rightarrow +\infty} \frac{f(x)}{g(x)}, \quad \theta \neq 0, \, +\infty. \]
Тогда интегралы
\[ \int _a^{+\infty}f(x)dx, \quad \int _a^{+\infty}g(x)dx \]
сходятся или расходятся одновременно.
Рассмотрим интеграл
\[ I=\int _1^{+\infty}\frac{1}{x+\sin x}\,dx. \]
Подинтегральное выражение - положительная функция на интервале интегрирования. Далее, при $x \rightarrow +\infty$ имеем:
$\sin x$ является "малой" поправкой в знаменателе. Точнее, если взять $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$, то
\[ \lim _{x \rightarrow +\infty}\frac{f(x)}{g(x)}=\lim _{x \rightarrow +\infty}\frac{x}{x+\sin x}=1. \]
Применяя второй признак сравнения, приходим к выводу, что наш интеграл сходится или расходится одновременно с интегралом
\[ \int _1^{+\infty}\frac{1}{x}\,dx . \]
Как было показано в предыдущем примере, этот интеграл расходится ($k=1$). Следовательно, исходный интеграл расходится.
Вычислить несобственный интеграл или установить его сходимость (расходимость).
1. \[ \int _{0}^{+\infty}e^{-ax}\,dx. \] 2. \[ \int _{0}^{+\infty}xe^{-x^2}\,dx. \] 3. \[ \int _{-\infty}^{+\infty}\frac{2xdx}{x^2+1}. \] 4. \[ \int _{0}^{+\infty}\frac{xdx}{(x+2)^3}. \] 5. \[ \int _{-\infty}^{+\infty}\frac{dx}{x^2+2x+2}. \] 6. \[ \int _{1}^{+\infty}\frac{lnx}{x^2}\,dx. \] 7. \[ \int _{1}^{+\infty}\frac{dx}{(1+x)\sqrt{x}}. \] 8. \[ \int _{0}^{+\infty}e^{-\sqrt{x}}\,dx. \] 9. \[ \int _{0}^{+\infty}e^{-ax}\cos x\,dx. \] 10. \[ \int _{0}^{+\infty}\frac{xdx}{x^3+1}. \]
Несобственные интегралы первого рода. По сути это тот же определённый интеграл, но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела интегрирования бесконечны.
Несобственные интегралы второго рода. По сути это тот же определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет, обращаясь в бесконечность.
Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.
Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже - красного цвета), x = a и осью абсцисс.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.
Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.
Несобственные интегралы первого рода - с бесконечными пределами и их сходимость
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.
.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл (если он сходится).
Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень икса - не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?
Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
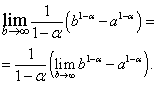
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при
имеет место .
Если , то
и
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница 
,
можно вывести следующую очень похожую на неё формулу:
.
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл (если он сходится).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:
Несобственные интегралы второго рода - от неограниченных функций и их сходимость
Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.
Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.
Используя формулу Ньютона-Лейбница, выводим.